同一系列的神经网络 和无监督学习 相关笔记点击查看
机器学习两种常见算法
监督学习Supervised Learning
监督学习的目的是根据给定的数据集,来预测某一个想知道的结果,而数据集中的每一个数据都是有对应结果的。来看两个例子:
在预测房价的数据集中,保存着如100平米的房子的售价是1000万元、300平米的房子的售价是2500万元这样的信息。这里我们想知到的结果就是x平米的房子能卖多少钱,比如我们输入200,希望得到一个价格。
在乳腺癌的数据集中,记录着如肿瘤大小为0.75mm是恶性的、肿瘤大小为0.01mm是良性的这种信息。这里我们想知道结果就是一个x大小的肿瘤是否为良性,比我我们输入0.45,希望他告诉我们是良性还是恶性。
回归问题Regression
在上述第一个举例中,我们要预测的房价其实是一种连续值 ,可以从几百万到几千万不等。回归问题 连续值问题
分类问题Classification
在上述第二个举例中,我们要判断的是一个肿瘤是否为良性,只可能有两种结果,要么是良性,要么不是良性,明显这是一个离散值 。分类问题 离散值问题
无监督学习Unsupervised Learning
无监督学习的目的是分析给定的数据集,寻找数据集中各数据的关系而不是想要得到一个结果。
比如监督学习中预测房价的例子,监督学习做的是根据数据集中的房子大小这一特征来预测某一大小房子的价格。
而在无监督学习中,房子大小和房子价格都会作为房子的特征,来分析房子之间的关系。比如他也许会将房子面积很大价格很高的那些房子归为一类,将房子面积很小但价格很高又归为一类等等.
下面是Google news的一部分,可以看到新闻被分为了很多类别,这也许就可以用无监督学习分析每个新闻的特征,将特征相似的新闻归为一类:
线性回归模型
单变量线性回归
先介绍几个符号以便说明:
m:训练样本的数量
x:输入变量(或特征)
y:输出变量(或目标变量)
hypothesis函数
单变量线性回归模型中,我们的目标是找到一条线性的hypothesis函数f w , b ( x ) = w x + b f_{w,b}(x)= wx + b f w , b ( x ) = w x + b w 、 b w、b w 、 b w 、 b w、b w 、 b f w , b ( x ) f_{w,b}(x) f w , b ( x )
cost function代价函数
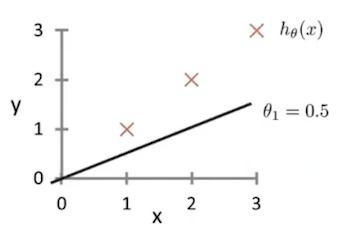
可以选取均方误差函数J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 J(\vec{w},b) = \frac{1}{2m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})^2} J ( w , b ) = 2 m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 b 和 w b和w b 和 w f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w},b} (\vec{x}^{(i)}) f w , b ( x ( i ) ) y ( i ) y^{(i)} y ( i ) f w ⃗ , b ( x ⃗ ) = 0.5 x f_{\vec{w},b}(\vec{x})=0.5x f w , b ( x ) = 0.5 x b = 0 , w = 0.5 b=0,w=0.5 b = 0 , w = 0.5
则J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 ≈ 0.58 J(\vec{w},b) = \frac{1}{2m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})^2}\approx 0.58 J ( w , b ) = 2 m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 ≈ 0.58
当然,不难看出当w = 1 、 b = 0 w=1、b=0 w = 1 、 b = 0 J ( w ⃗ , b ) = 0 J(\vec{w},b) = 0 J ( w , b ) = 0 b 、 w b 、 w b 、 w
上边的情况实际上我所选择的样本可以使b = 0 b=0 b = 0 w w w
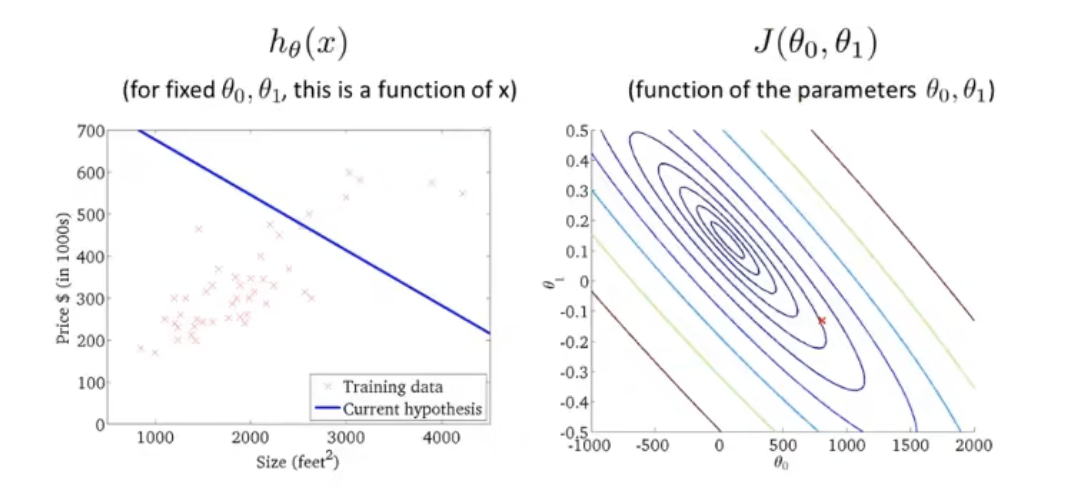
此时不难发现,J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) w 、 b w、b w 、 b J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) f w ⃗ , b ( x ⃗ ) f_{\vec{w},b}(\vec{x}) f w , b ( x )
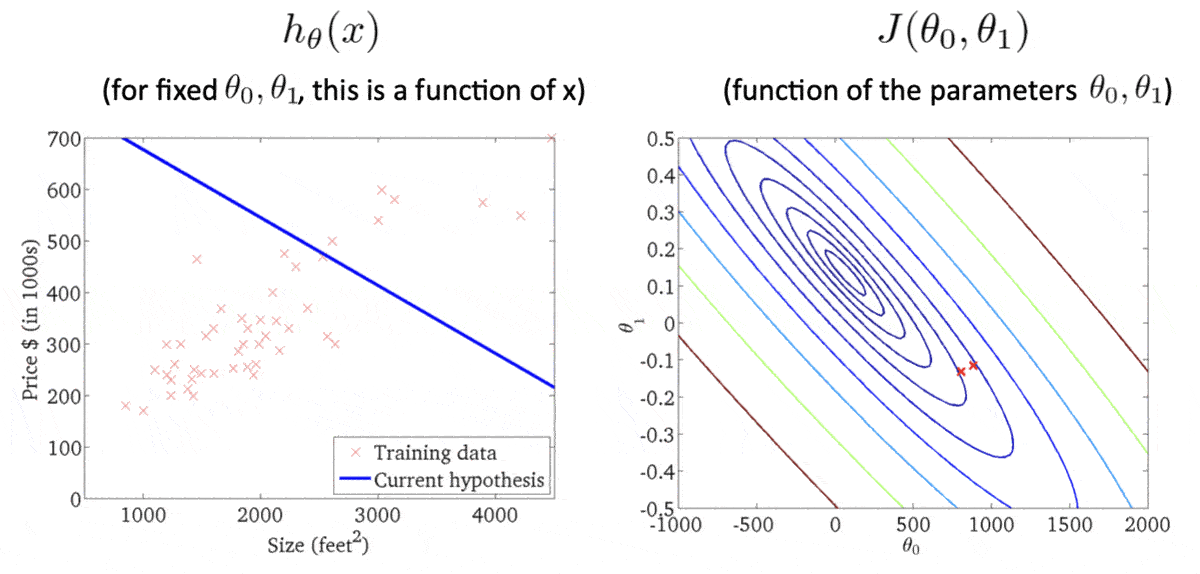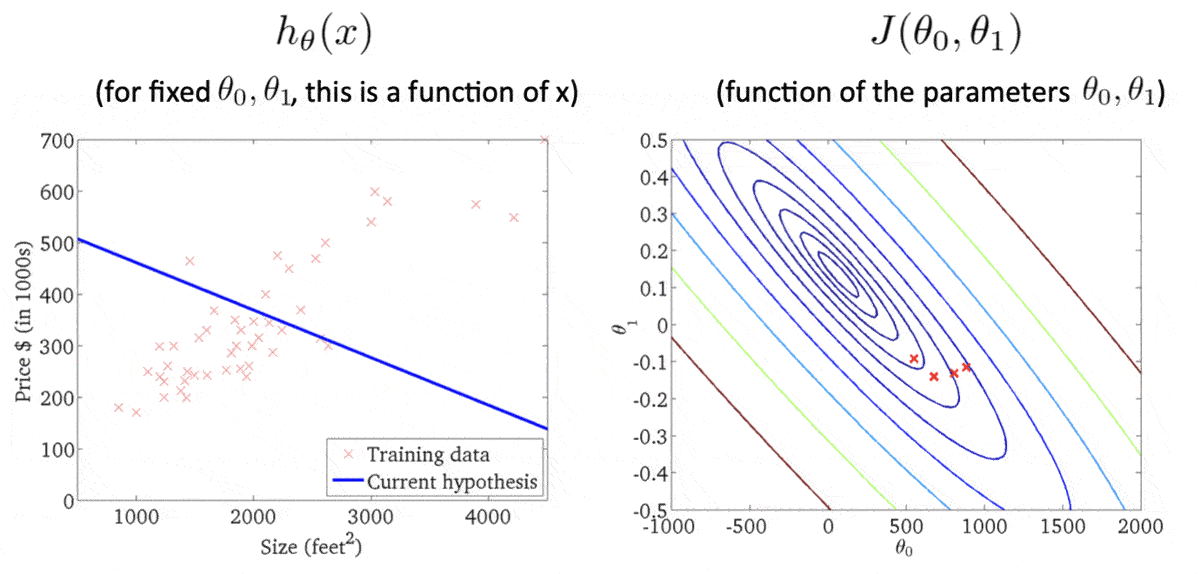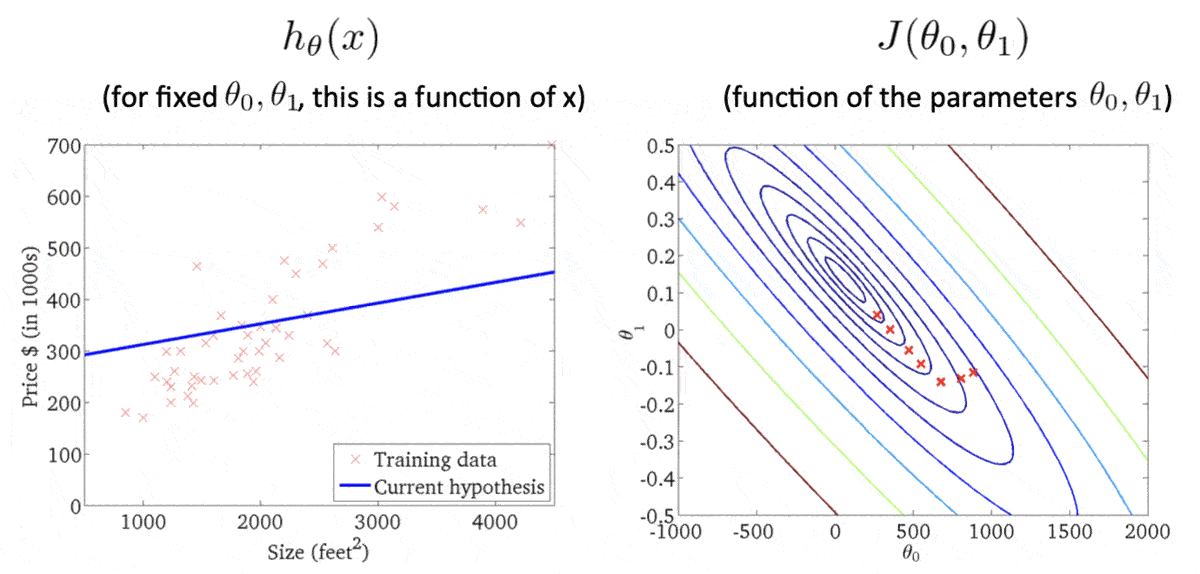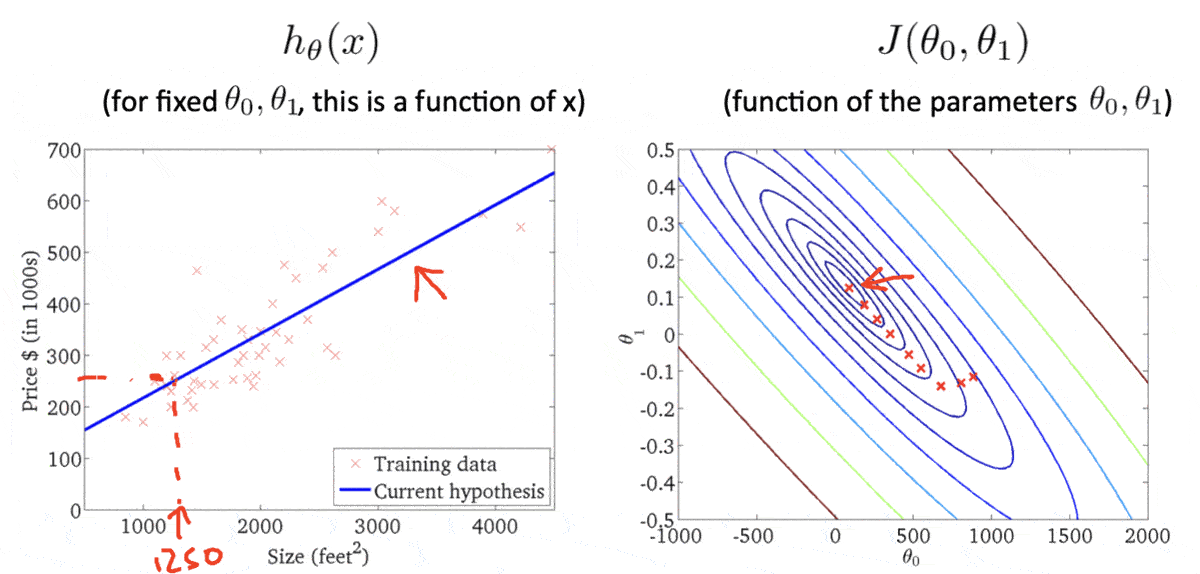
等高线各椭圆的中心是我们的目标,此时我们得到的点(右图的红叉❌)很明显举例目标还有一段距离,因此反映在左图中,得到的假设函数与数据集的拟合程度肉眼可见的差。此时便需要重新计算w 、 b w、b w 、 b
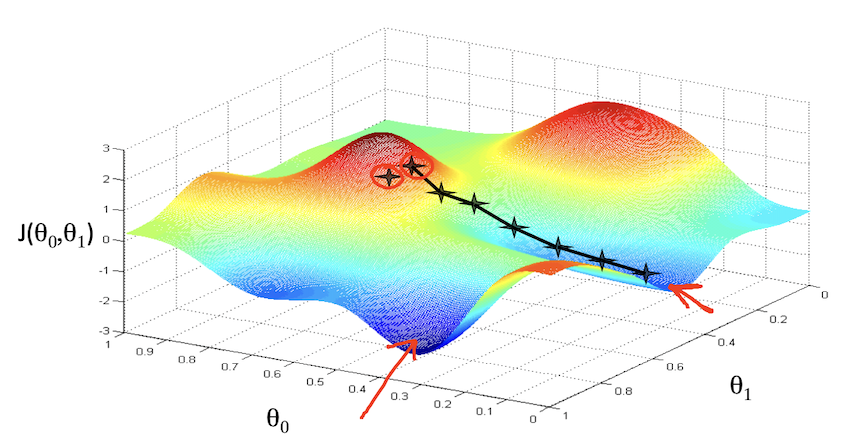
Gradient descent梯度下降算法
使用梯度下降算法可以一次次迭代,最终找到可以使得J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) w 、 b w、b w 、 b J ( w 1 , w 2 , . . . , w n , b ) J(w_1,w_2,...,w_n,b) J ( w 1 , w 2 , ... , w n , b )
单变量梯度下降算法描述如下:
r e p e a t u n t i l c o n v e r g e n c e { repeat\quad until\quad convergence \quad\{ re p e a t u n t i l co n v er g e n ce {
w = w − α ∂ J ( w ⃗ , b ) ∂ w \quad\quad w=w-\alpha\frac{\partial J(\vec{w},b)}{\partial w} w = w − α ∂ w ∂ J ( w , b ) b = b − α ∂ J ( w ⃗ , b ) ∂ b \quad\quad b=b -\alpha\frac{\partial J(\vec{w},b)}{\partial b} b = b − α ∂ b ∂ J ( w , b )
} \} }
其中α \alpha α w 、 b w、b w 、 b α \alpha α w 、 b w、b w 、 b
另外再仔细观察一下该算法和J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) 更新参数都遍历了整个样本 小批量梯度下降 ,是现在常用的一种方法。
w 、 b w、b w 、 b 二者要同时变化而不能先变一个,另一个再变
Correct:
t e m p _ w = w − α ∂ J ( w ⃗ , b ) ∂ w temp\_w=w-\alpha\frac{\partial J(\vec{w},b)}{\partial w} t e m p _ w = w − α ∂ w ∂ J ( w , b )
t e m p _ b = b − α ∂ J ( w ⃗ , b ) ∂ b temp\_b=b-\alpha\frac{\partial J(\vec{w},b)}{\partial b} t e m p _ b = b − α ∂ b ∂ J ( w , b )
w = t e m p _ w w=temp\_w w = t e m p _ w
b = t e m p _ b b=temp\_b b = t e m p _ b
Incorrect:
t e m p _ w = w − α ∂ J ( w ⃗ , b ) ∂ w temp\_w=w-\alpha\frac{\partial J(\vec{w},b)}{\partial w} t e m p _ w = w − α ∂ w ∂ J ( w , b )
w = t e m p _ w w=temp\_w w = t e m p _ w
t e m p _ b = b − α ∂ J ( w ⃗ , b ) ∂ b temp\_b=b-\alpha\frac{\partial J(\vec{w},b)}{\partial b} t e m p _ b = b − α ∂ b ∂ J ( w , b )
b = t e m p _ b b=temp\_b b = t e m p _ b
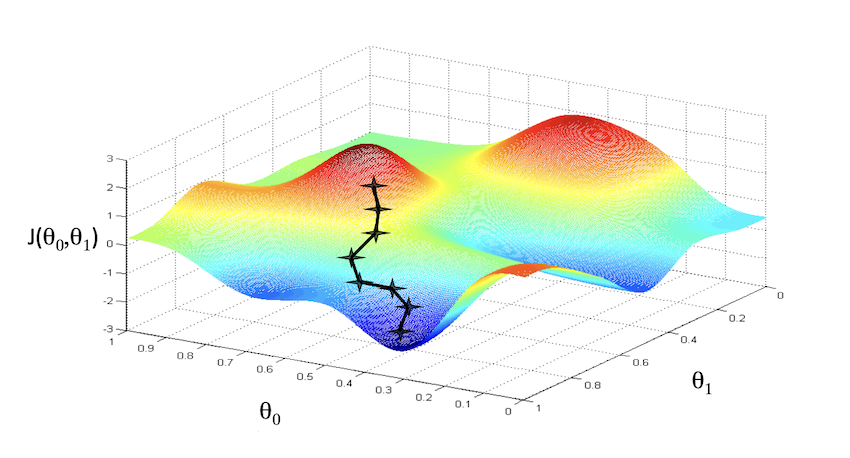
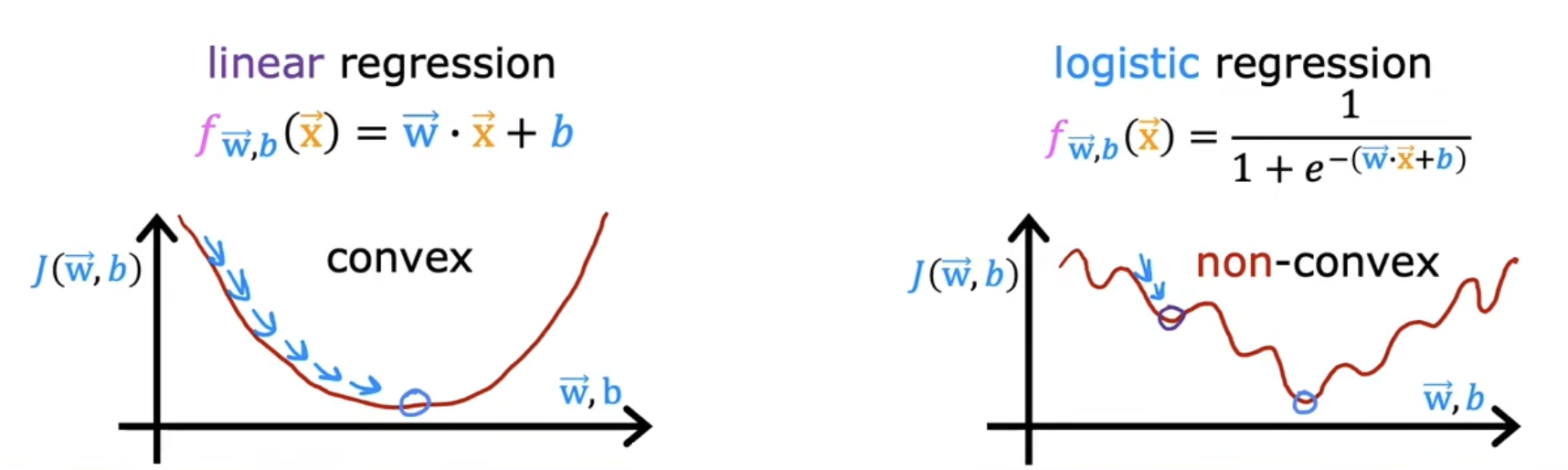
对于一般的代价函数,其形状不一定是图函数,因此对于不同的起点,可能找到不同的局部最优点:
尽管起点相差很小,但最终得到的代价函数完全不一样。
将该算法应用到线性回归模型中:
说明一点:线性回归的代价函数总是一个凸函数,因此他不会出现一般代价函数的局部最优的情况,他总会收敛到全局最优。
f w ⃗ , b ( x ⃗ ) = w ⃗ x ⃗ + b f_{\vec{w},b}(\vec{x})=\vec{w} \vec{x}+b f w , b ( x ) = w x + b
J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 J(\vec{w},b) = \frac{1}{2m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})^2} J ( w , b ) = 2 m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2
w : ∂ J ( w ⃗ , b ) ∂ w = 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x ( i ) w:\frac{\partial J(\vec{w},b)}{\partial w}=\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})x^{(i)}} w : ∂ w ∂ J ( w , b ) = m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x ( i )
b : ∂ J ( w ⃗ , b ) ∂ b = 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) b:\frac{\partial J(\vec{w},b)}{\partial b}=\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})} b : ∂ b ∂ J ( w , b ) = m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) )
Gradient descent algorithm:
r e p e a t u n t i l c o n v e r g e n c e { repeat\quad until\quad convergence\quad \{ re p e a t u n t i l co n v er g e n ce {
w = w − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x ( i ) \quad\quad w=w-\alpha\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})x^{(i)}} w = w − α m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x ( i )
b = b − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) \quad\quad b=b-\alpha\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})} b = b − α m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) )
} \} }
这样就得到了一条拟合程度还不错的假设函数。
多变量线性回归
向量化多特征
实际情况往往不仅含一个特征,比如房价的预测不仅仅和房子大小有关,也和楼层、层高、位置等有关,此时就会出现多个特征。而要对多个特征逐一使用梯度下降算法的话,不仅代码冗长,且运算速度慢。为了解决这个问题,可以将多个特征记为向量x ⃗ = ( x 1 , x 2 , . . . , x n ) \vec{x}=(x_1,x_2,...,x_n) x = ( x 1 , x 2 , ... , x n ) f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b . f_{\vec{w},b}(\vec{x})=\vec{w} \cdot \vec{x}+b. f w , b ( x ) = w ⋅ x + b .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 def my_dot (a, b ): """ Compute the dot product of two vectors Args: a (ndarray (n,)): input vector b (ndarray (n,)): input vector with same dimension as a Returns: x (scalar): """ x=0 for i in range (a.shape[0 ]): x = x + a[i] * b[i] return x np.random.seed(1 ) a = np.random.rand(10000000 ) b = np.random.rand(10000000 ) tic = time.time() c = np.dot(a, b) toc = time.time() print (f"np.dot(a, b) = {c:.4 f} " )print (f"Vectorized version duration: {1000 *(toc-tic):.4 f} ms " )tic = time.time() c = my_dot(a,b) toc = time.time() print (f"my_dot(a, b) = {c:.4 f} " )print (f"loop version duration: {1000 *(toc-tic):.4 f} ms " )del (a);del (b)
1 2 3 4 5 np.dot(a, b) = 2501072.5817 Vectorized version duration: 13.3328 ms my_dot(a, b) = 2501072.5817 loop version duration: 1374.0389 ms
可以看出,本例中运算速度相差了100倍左右。
Normal equation正规方程求解w、b
在说明多特征值线性回归梯度下降算法之前,介绍一种快速求解线性回归问题 中w、b的方法:正规方程法。相较于梯度下降算法,正规方程有以下下局限性:
同时也有一些优点:
不需要设置学习率α \alpha α
不需要迭代,对于规模较小的特征,有不错的效率
具体实现,留白,有空回来补
多特征线性回归梯度下降算法
和单特征线性回归梯度下降算法相似,只不过多了几个特征而已:
r e p e a t u n t i l c o n v e r g e n c e { repeat\quad until\quad convergence \quad\{ re p e a t u n t i l co n v er g e n ce {
w 1 = w 1 − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x 1 ( i ) \quad\quad w_1=w_1-\alpha\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})x^{(i)}_1} w 1 = w 1 − α m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x 1 ( i )
w 2 = w 2 − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x 2 ( i ) \quad\quad w_2=w_2-\alpha\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})x^{(i)}_2} w 2 = w 2 − α m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x 2 ( i )
⋮ \quad\quad\quad \vdots ⋮
w n = w n − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x n ( i ) \quad\quad w_n=w_n-\alpha\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})x^{(i)}_n} w n = w n − α m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x n ( i )
b = b − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) \quad\quad b=b -\alpha\frac{1}{m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})} b = b − α m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) )
} \} }
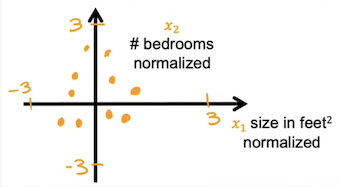
特征缩放
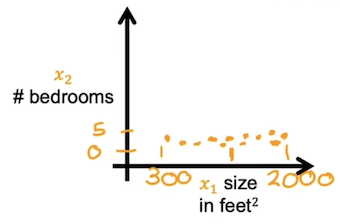
当多个特征的取值范围相差很大时,梯度下降算法运行的很慢,此时需要将多个特征值缩放到一个相近的范围内,同时保证这个范围不要太大像-100-100,或者太小像-0.0001-0.0001.
比如现在有两个特征房子的大小300 ⩽ x 1 ⩽ 1000 300\leqslant x_1 \leqslant1000 300 ⩽ x 1 ⩽ 1000 0 ⩽ x 2 ⩽ 6 0\leqslant x_2\leqslant6 0 ⩽ x 2 ⩽ 6
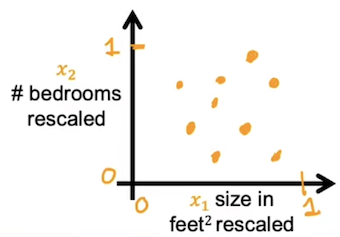
除以最大值
比较简单的一个方法,就是将各特征除以该特征的最大值,这样就可以得到的新特征的范围便可以满足要求。x 1 x_1 x 1 x 2 x_2 x 2 0.3 ⩽ x 1 , s c a l e d ⩽ 1 0.3\leqslant x_{1,scaled} \leqslant1 0.3 ⩽ x 1 , sc a l e d ⩽ 1 0 ⩽ x 2 , s c a l e d ⩽ 1 0\leqslant x_{2,scaled} \leqslant 1 0 ⩽ x 2 , sc a l e d ⩽ 1
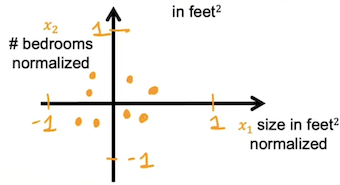
Mean normalization
均值归一化首先要计算每个特征的平均值μ i \mu_i μ i x i x_i x i x i , s c a l e d = x i − μ i M a x − M i n x_{i,scaled}=\frac{x_i - \mu_i}{Max-Min} x i , sc a l e d = M a x − M in x i − μ i M a x 、 M i n Max、Min M a x 、 M in
Z-score normalize
Z-score归一化首先要计算每个特征的平均值μ i \mu_i μ i σ i \sigma_i σ i x i x_i x i x i , s c a l e d = x i − μ i σ i x_{i,scaled}=\frac{x_i-\mu_i}{\sigma_i} x i , sc a l e d = σ i x i − μ i
下面举个例子判断一下某个特征是否需要rescale:
0 ⩽ x 1 ⩽ 3 、 − 2 ⩽ x 2 ⩽ 0.5 、 − 100 ⩽ x 3 ⩽ 100 、 − 0.001 ⩽ x 1 ⩽ 0.001 、 98.6 ⩽ x 1 ⩽ 105 0\leqslant x_1\leqslant3、-2\leqslant x_2\leqslant0.5、-100\leqslant x_3\leqslant100、-0.001\leqslant x_1\leqslant0.001、98.6\leqslant x_1\leqslant105 0 ⩽ x 1 ⩽ 3 、 − 2 ⩽ x 2 ⩽ 0.5 、 − 100 ⩽ x 3 ⩽ 100 、 − 0.001 ⩽ x 1 ⩽ 0.001 、 98.6 ⩽ x 1 ⩽ 105
简单判断一下,其实x 1 、 x 2 x_1、x_2 x 1 、 x 2 x 3 、 x 4 、 x 5 x_3、x_4、x_5 x 3 、 x 4 、 x 5 x 1 、 x 2 x_1、x_2 x 1 、 x 2
如果一个特征的范围比较暧昧,对他进行放缩就可以,因为放缩到合适的尺度不会对算法有什么负面效果。
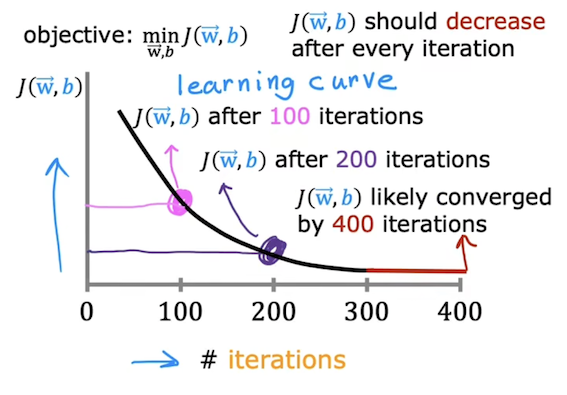
判断梯度下降是否收敛
一个方法是可以观察y轴为J ( w ⃗ , b ) J(\vec{w},b) J ( w , b )
当迭代次数达到400时,斜率几乎为0,此时便可以判断出函数J ( w ⃗ , b ) J(\vec{w},b) J ( w , b )
另一个方法是自动收敛测试,该方法需要选择一个合适的ε \varepsilon ε J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) ε \varepsilon ε w ⃗ , b \vec{w},b w , b ε \varepsilon ε
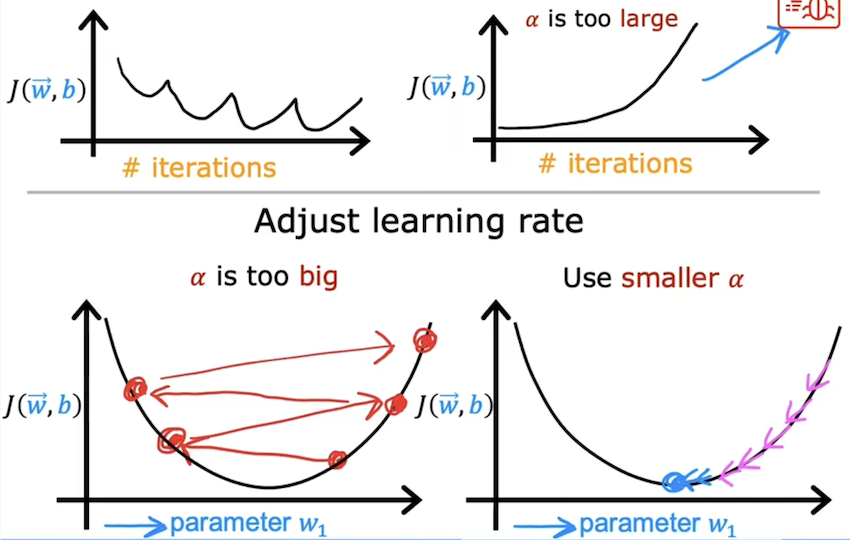
学习率的设置
直观来讲,学习率是一个影响代价参数w ⃗ , b \vec{w},b w , b J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) J ( w ⃗ , b ) J(\vec{w},b) J ( w , b )
通常可以依次尝试这几个学习率:0.001、0.003、0.01、0.03、0.1、0.3、1、…
即从0.001开始,每次扩大大约3倍,或者缩小3倍左右。
这样一次次尝试后,可以找到一个最大值和一个最小值,为了使收敛的速度更快一些,可以选择比找到的最大值小一些的可以使J ( w ⃗ , b ) J(\vec{w},b) J ( w , b ) α \alpha α
特征工程
特征工程就是将原本的一些特征进行组合,得到一些新的特征,这样也许可以使模型更加精准。
如原数据集中有房子的长和宽两个特征x 1 、 x 2 x_1、x_2 x 1 、 x 2 f w ⃗ , b ( x ⃗ ) = w 1 x 1 + w 2 x 2 + b f_{\vec{w},b}(\vec{x})=w_1x_1+w_2x_2+b f w , b ( x ) = w 1 x 1 + w 2 x 2 + b
现在我们可以让x 3 = x 1 × x 2 x_3=x_1 \times x_2 x 3 = x 1 × x 2 f w ⃗ , b ( x ⃗ ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + b f_{\vec{w},b}(\vec{x})=w_1x_1+w_2x_2+w_3x_3+b f w , b ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + b
多项式回归
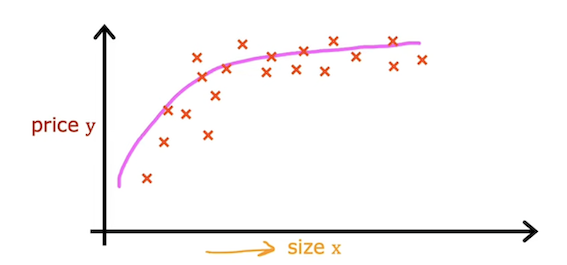
线性回归中我们使用线性函数来拟合数据集,多项是回归中,我们可以使用非线性的函数来拟合数据集。
如图,这个数据集如果用线性函数来拟合的话,很明显不太合适。可以选择f w ⃗ , b ( x ) = w 1 x + w 2 x + b f_{\vec{w},b}(x)=w_1x+w_2 \sqrt{x}+b f w , b ( x ) = w 1 x + w 2 x + b
需要注意的是,在使用多项式回归的时候,不同的特征范围的差别可能很大,比如对同一特征的平方和立方,这是要记得使用特征缩放让他们处于一个相对合理的范围。
逻辑回归模型
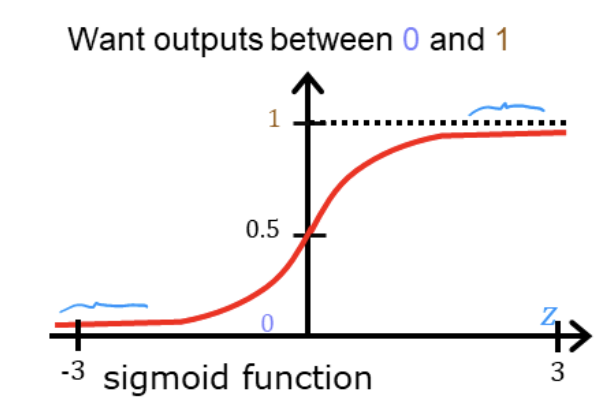
逻辑回归模型可用于二元分类问题 ,其形式为f w ⃗ , b ( x ⃗ ) = g ( z ) = 1 1 + e − z , f_{\vec{w},b}(\vec{x}) = g(z) = \frac{1}{1+e^{-z}}, f w , b ( x ) = g ( z ) = 1 + e − z 1 , z = w ⃗ ⋅ x ⃗ + b z=\vec{w} \cdot \vec{x}+b z = w ⋅ x + b lim z → − ∞ g ( z ) = 0 , lim z → + ∞ g ( z ) = 1 \displaystyle \lim_{z \to -\infin} g(z) = 0,\displaystyle \lim_{z \to +\infin} g(z) = 1 z → − ∞ lim g ( z ) = 0 , z → + ∞ lim g ( z ) = 1 y ^ \hat{y} y ^ 某事件发生的概率 ,则P ( y = 1 ∣ x ; w ⃗ , b ) + P ( y = 0 ∣ x ; w ⃗ , b ) = 1. P(y=1|x;\vec{w},b)+P(y=0|x;\vec{w},b)=1. P ( y = 1∣ x ; w , b ) + P ( y = 0∣ x ; w , b ) = 1.
我们可以设置一个threshold=0.5,当0 < g ( z ) < 0.5 0<g(z)<0.5 0 < g ( z ) < 0.5 y ^ = 0 \hat{y} = 0 y ^ = 0 0.5 ≤ g ( z ) < 1 0.5 \le g(z)<1 0.5 ≤ g ( z ) < 1 y ^ = 1 \hat{y} = 1 y ^ = 1
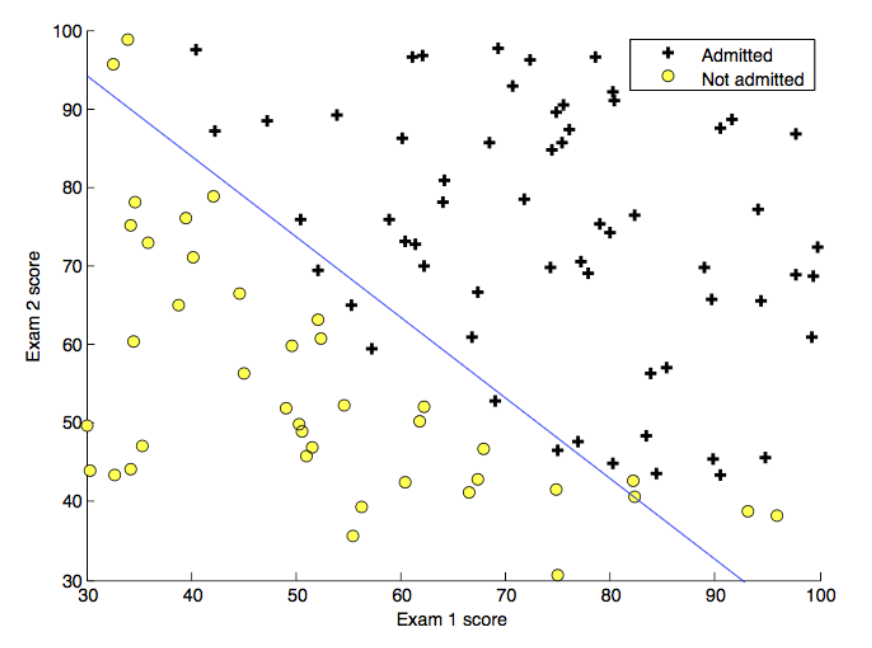
可以看出当z = 0 z=0 z = 0 g ( z ) = 0.5 g(z)=0.5 g ( z ) = 0.5 z = w ⃗ ⋅ x ⃗ + b = 0 z=\vec{w} \cdot \vec{x}+b=0 z = w ⋅ x + b = 0 决策边界 w ⃗ , x ⃗ \vec{w},\vec{x} w , x
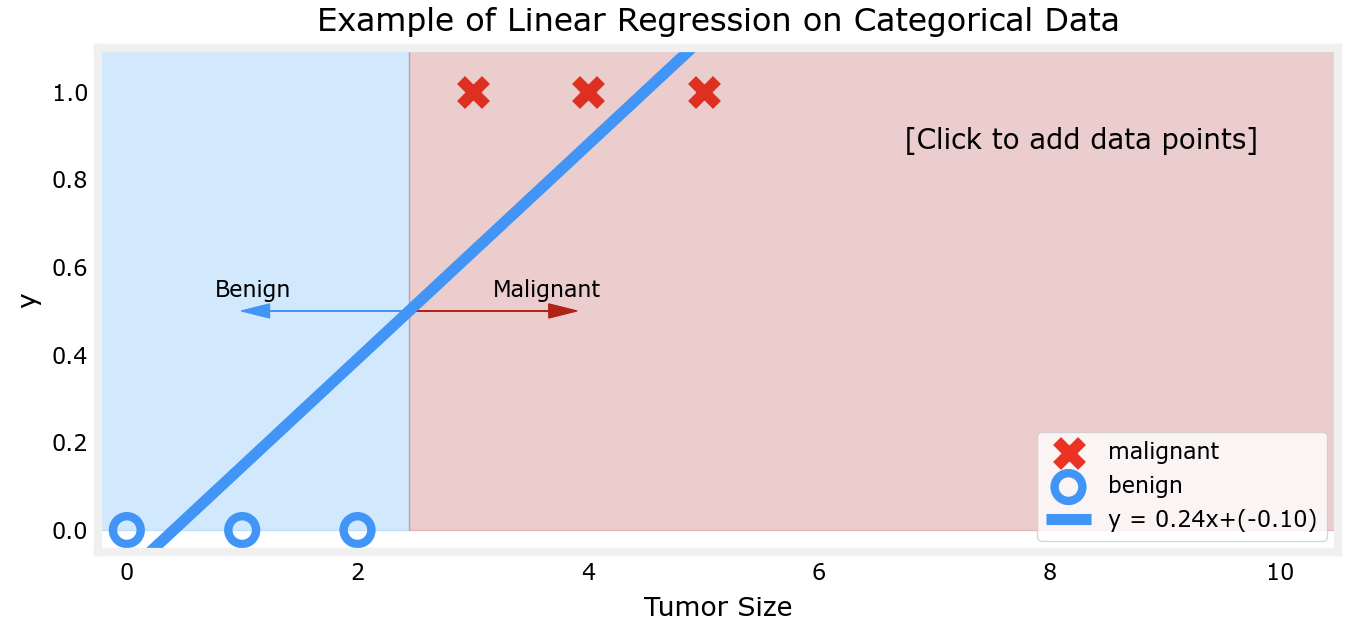
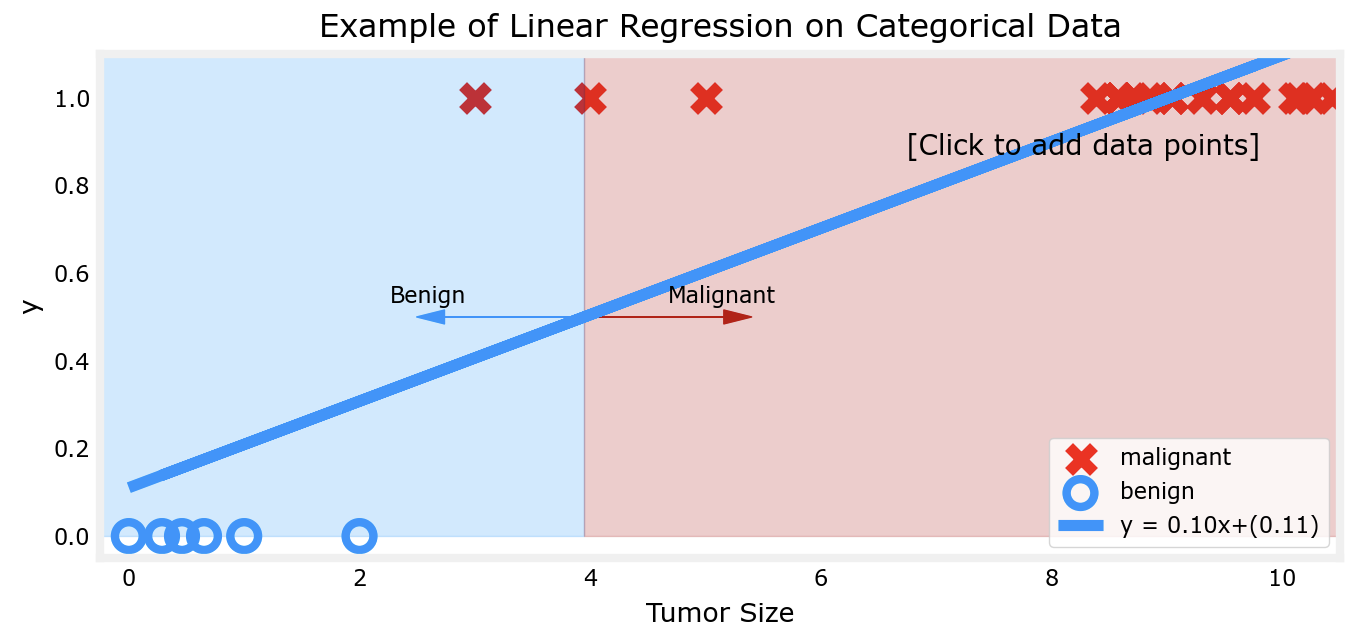
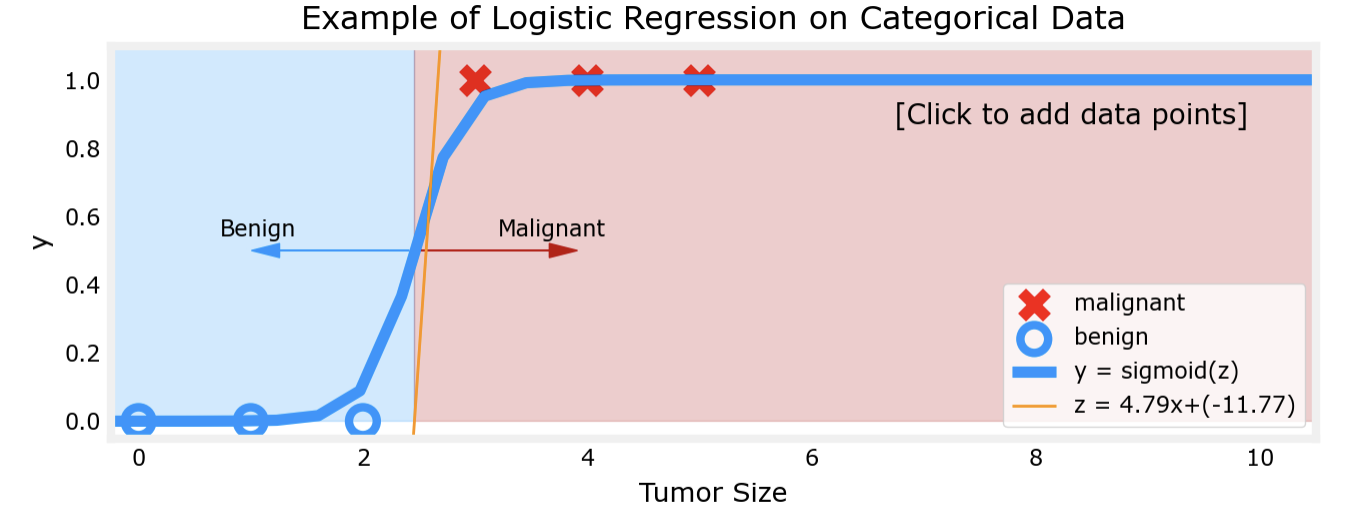
下面以肿瘤为例看一下为什么对于二元分类问题,线性回归模型不能解决:
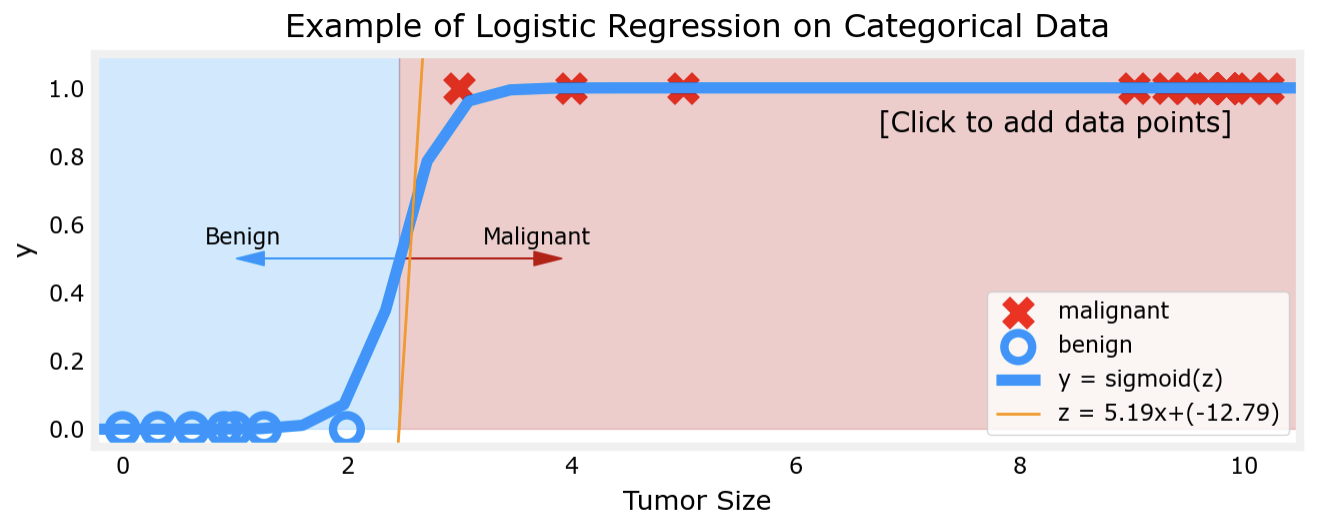
对比以上两幅图片不难看出,若肿瘤大小分别在较小处和较大处的聚集,线性回归对于肿瘤性质的判断会出现越来越大的误差,这显然是不正确的。而逻辑回归模型则可以解决这一问题:
可以看出,逻辑回归模型在两端数据聚集时的表现仍然出色。
代价函数
线性回归中使用平方误差函数J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 J(\vec{w},b) = \frac{1}{2m}\sum_{i=1}^m {(f_{\vec{w},b} (\vec{x}^{(i)}) - y^{(i)})^2} J ( w , b ) = 2 m 1 ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2
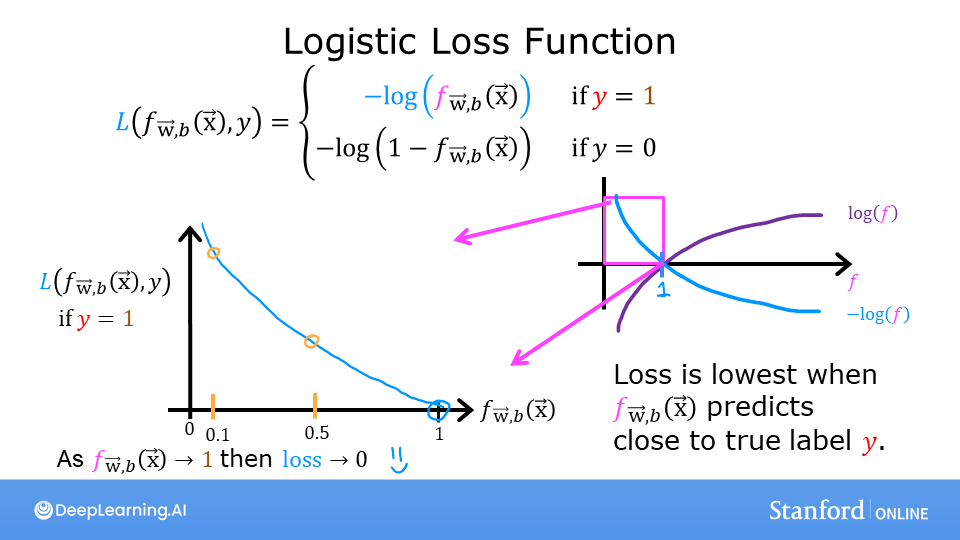
逻辑回归中的代价函数为J ( w ⃗ , b ) = 1 m ∑ i = 0 m − 1 [ l o s s ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) ] J(\vec{w},b) = \frac{1}{m} \sum_{i=0}^{m-1} \left[ loss(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) \right] J ( w , b ) = m 1 ∑ i = 0 m − 1 [ l oss ( f w , b ( x ( i ) ) , y ( i ) ) ]
l o s s ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = { − log ( f w ⃗ , b ( x ⃗ ( i ) ) ) , i f y ( i ) = 1 − log ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) , i f y ( i ) = 0 loss(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) = \left\{\begin{matrix}
-\log\left(f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right), & if \quad y^{(i)}=1\\
-\log \left( 1 - f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right), & if \quad y^{(i)}=0\\
\end{matrix}\right. l oss ( f w , b ( x ( i ) ) , y ( i ) ) = { − log ( f w , b ( x ( i ) ) ) , − log ( 1 − f w , b ( x ( i ) ) ) , i f y ( i ) = 1 i f y ( i ) = 0
可化简为:
l o s s ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = − y ( i ) log ( f w ⃗ , b ( x ⃗ ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) loss(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) = -y^{(i)} \log\left(f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right)
l oss ( f w , b ( x ( i ) ) , y ( i ) ) = − y ( i ) log ( f w , b ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − f w , b ( x ( i ) ) )
l o s s ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) loss(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) l oss ( f w , b ( x ( i ) ) , y ( i ) ) J ( ) J() J ( ) 0 ≤ f w ⃗ , b ( x ⃗ ( i ) ) ≤ 1 0 \le f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \le 1 0 ≤ f w , b ( x ( i ) ) ≤ 1
可以看出:
i f y = 1 if \quad y=1 i f y = 1
若f w ⃗ , b ( x ⃗ ( i ) ) → 1 , l o s s ( ) → 0 f_{\vec{w},b}(\vec{x}^{(i)}) \rightarrow1,loss() \rightarrow0 f w , b ( x ( i ) ) → 1 , l oss ( ) → 0
若f w ⃗ , b ( x ⃗ ( i ) ) → 0 , l o s s ( ) → ∞ f_{\vec{w},b}(\vec{x}^{(i)}) \rightarrow 0,loss() \rightarrow \infin f w , b ( x ( i ) ) → 0 , l oss ( ) → ∞
而此时y = 1 y=1 y = 1 f w ⃗ , b ( x ⃗ ( i ) ) → 1 f_{\vec{w},b}(\vec{x}^{(i)}) \rightarrow 1 f w , b ( x ( i ) ) → 1
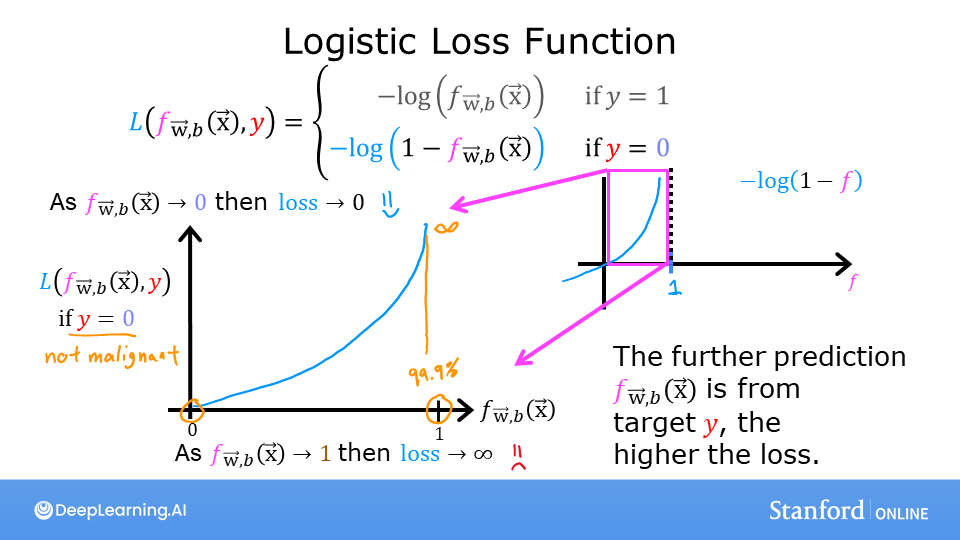
i f y = 0 if \quad y=0 i f y = 0
若f w ⃗ , b ( x ⃗ ( i ) ) → 0 , l o s s ( ) → 0 f_{\vec{w},b}(\vec{x}^{(i)}) \rightarrow 0,loss() \rightarrow 0 f w , b ( x ( i ) ) → 0 , l oss ( ) → 0
若f w ⃗ , b ( x ⃗ ( i ) ) → 1 , l o s s ( ) → ∞ f_{\vec{w},b}(\vec{x}^{(i)}) \rightarrow 1,loss() \rightarrow \infin f w , b ( x ( i ) ) → 1 , l oss ( ) → ∞
而此时y = 0 y=0 y = 0 f w ⃗ , b ( x ⃗ ( i ) ) → 0 f_{\vec{w},b}(\vec{x}^{(i)}) \rightarrow 0 f w , b ( x ( i ) ) → 0
别忘记了代价函数是要寻找参数w ⃗ 、 b , \vec{w}、b, w 、 b , l o s s ( ) → ∞ loss() \rightarrow \infin l oss ( ) → ∞ w ⃗ 、 b \vec{w}、b w 、 b w ⃗ 、 b . \vec{w}、b. w 、 b .
对了还有一点需要指出,高等数学中常用l n ln l n e e e l o g log l o g e e e
梯度下降
算法的原理与线性回归类似,只不过由于预测函数和代价函数都不一样:
repeat until convergence: { w j = w j − α ∂ J ( w ⃗ , b ) ∂ w j for j = 0,...,n-1 b = b − α ∂ J ( w ⃗ , b ) ∂ b } \begin{align*}
&\text{repeat until convergence:} \; \lbrace \\
& \; \; \;w_j = w_j - \alpha \frac{\partial J(\vec{w},b)}{\partial w_j} \; & \text{for j = 0,...,n-1} \\
& \; \; \; \; \;b = b - \alpha \frac{\partial J(\vec{w},b)}{\partial b} \\
&\rbrace
\end{align*} repeat until convergence: { w j = w j − α ∂ w j ∂ J ( w , b ) b = b − α ∂ b ∂ J ( w , b ) } for j = 0,...,n-1
其中:
∂ J ( w ⃗ , b ) ∂ w j = 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) ∂ J ( w ⃗ , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) \begin{align*}
\frac{\partial J(\vec{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \\
\frac{\partial J(\vec{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})
\end{align*} ∂ w j ∂ J ( w , b ) ∂ b ∂ J ( w , b ) = m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) = m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) )
于是,逻辑回归的梯度下降算法就变成了:
r e p e a t u n t i l c o n v e r g e n c e : { w j = w j − α 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) for j = 0,...,n-1 b = b − α 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) } s i m u l t a n e o u s u p d a t e s \begin{align*}
&repeat \quad until \quad convergence: \; \lbrace \\
& \; \; \;w_j = w_j - \alpha \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \; & \text{for j = 0,...,n-1} \\
& \; \; \; \; \;b = b - \alpha \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \\
&\rbrace simultaneous \quad updates
\end{align*} re p e a t u n t i l co n v er g e n ce : { w j = w j − α m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) b = b − α m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) } s im u lt an eo u s u p d a t es for j = 0,...,n-1
但是经过计算后会发现,即使代价函数不一样,但是对于w ⃗ 、 b \vec{w}、b w 、 b
L i n e a r r e g r e s s i o n : f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b Linear \quad regression: \quad f_{\vec{w},b}(\vec{x})=\vec{w} \cdot \vec{x}+b L in e a r re g ress i o n : f w , b ( x ) = w ⋅ x + b
L o g i s t i c r e g r e s s i o n : f w ⃗ , b ( x ⃗ ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) Logistic \quad regression: \quad f_{\vec{w},b}(\vec{x})=\frac{1}{1+e^{-(\vec{w} \cdot \vec{x}+b)}} L o g i s t i c re g ress i o n : f w , b ( x ) = 1 + e − ( w ⋅ x + b ) 1
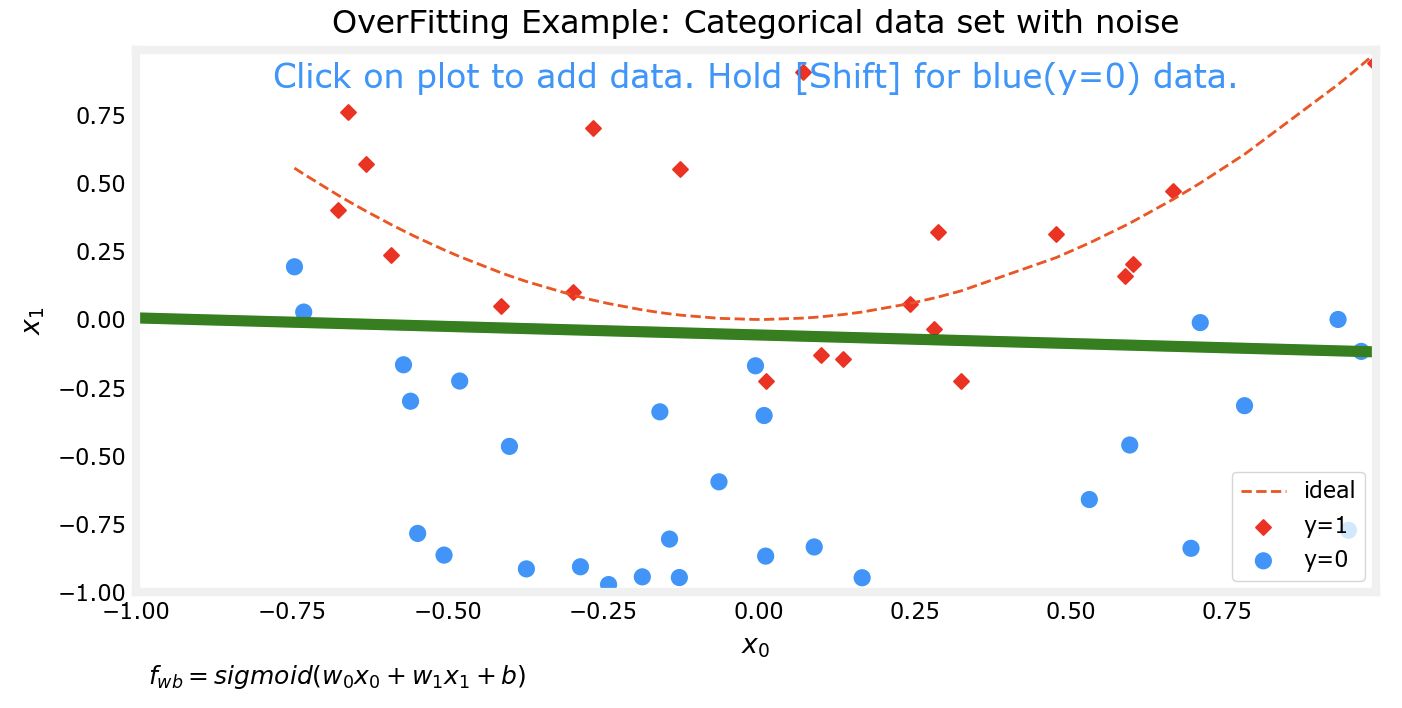
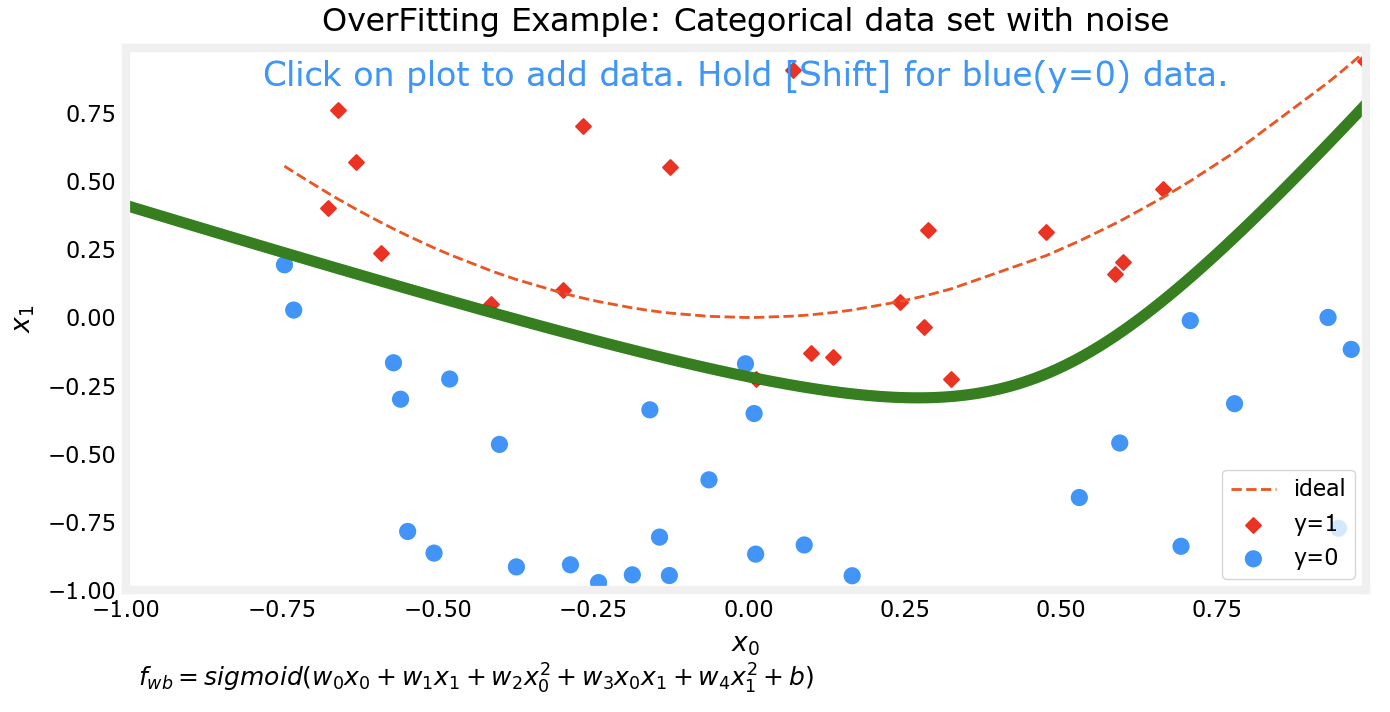
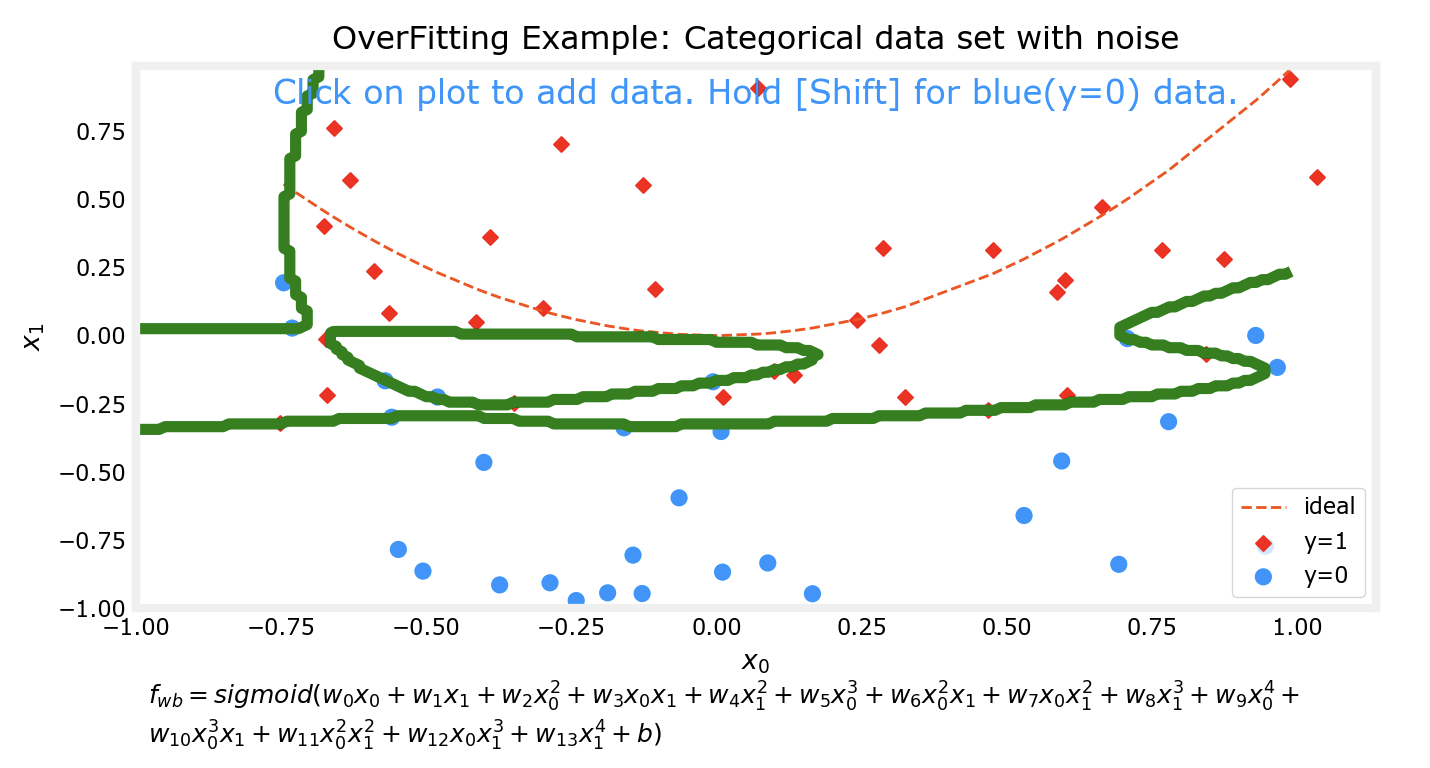
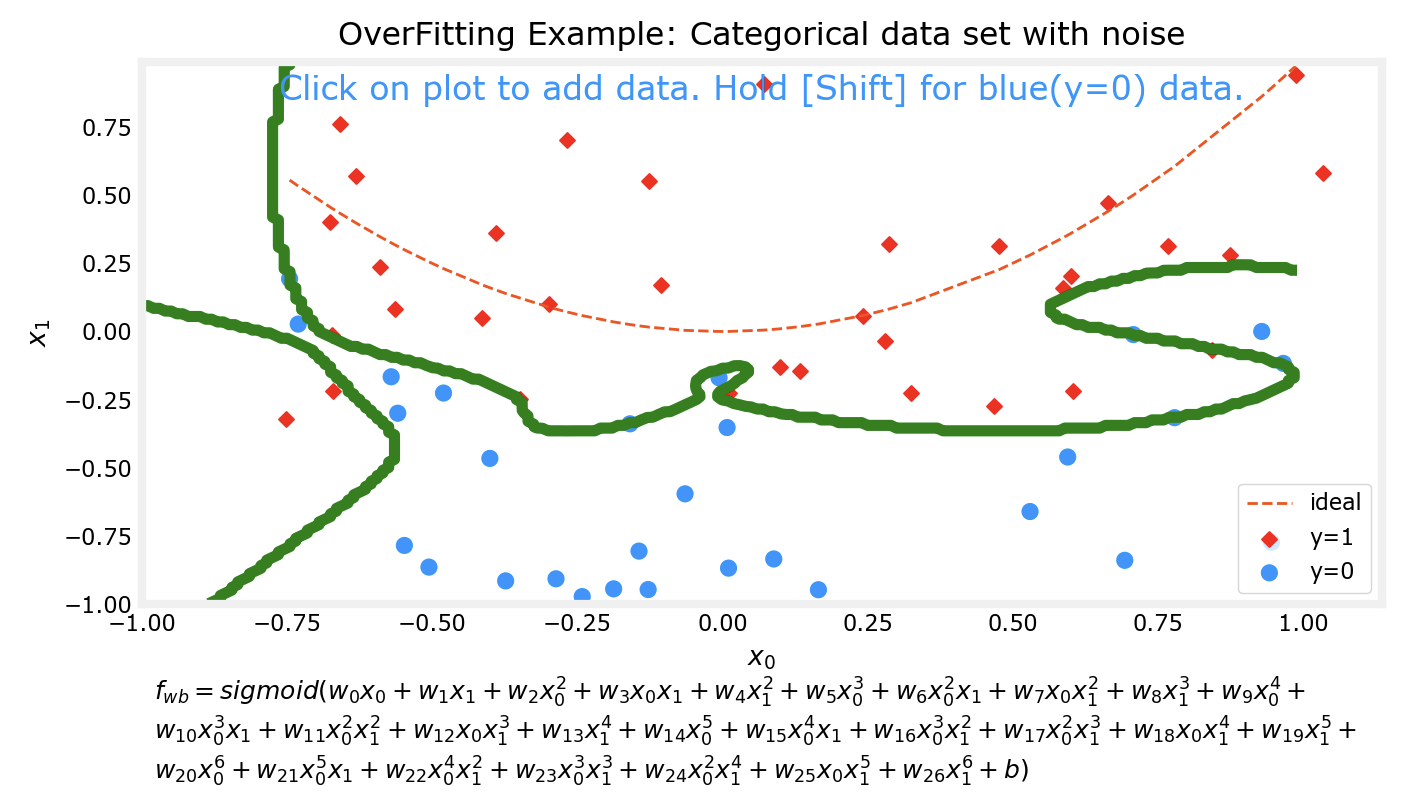
过拟合
对于预测模型,我们通常希望他能得到较为准确的预测结果,一个方法来提高准确性是通过多项式来拟合数据集。但是如果追求能完美拟合某数据集的模型,该模型往往会出现过拟合的现象。
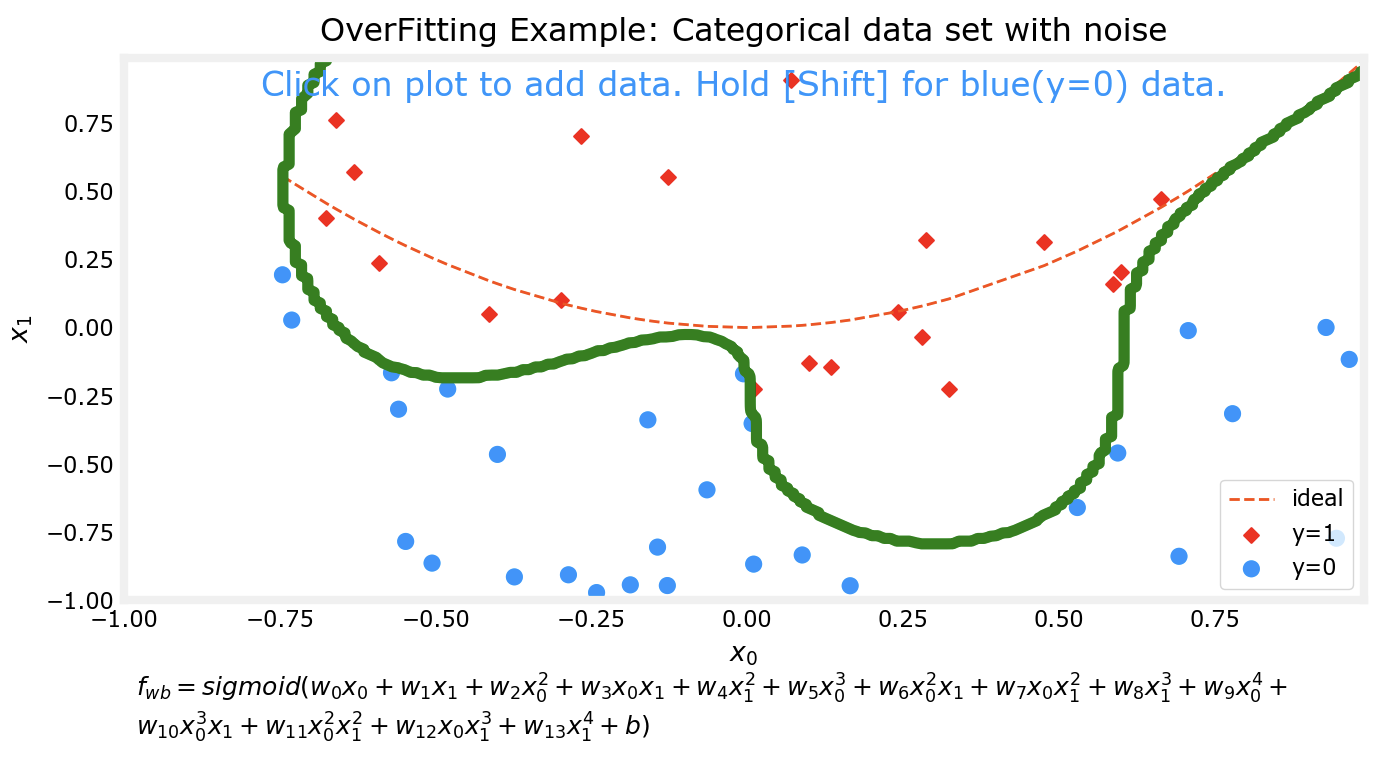
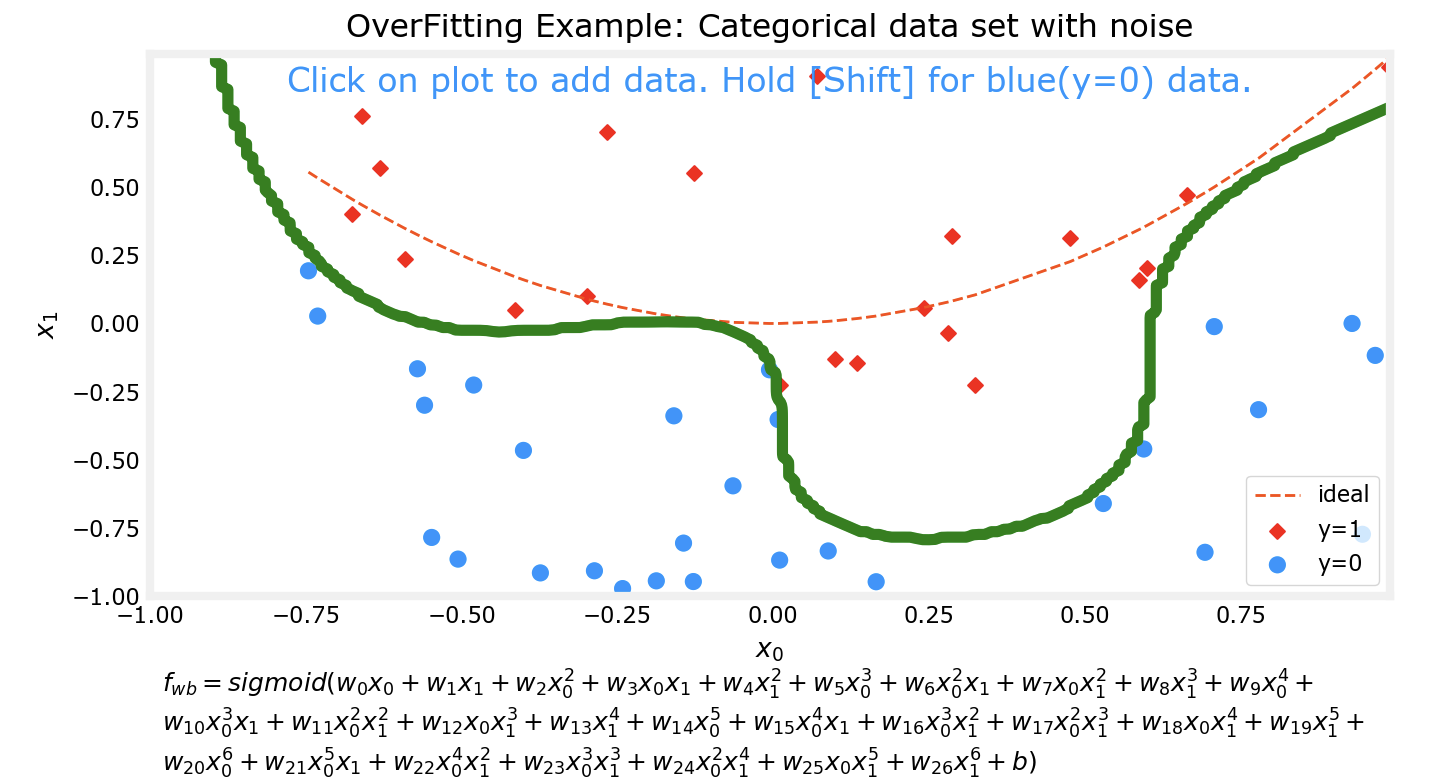
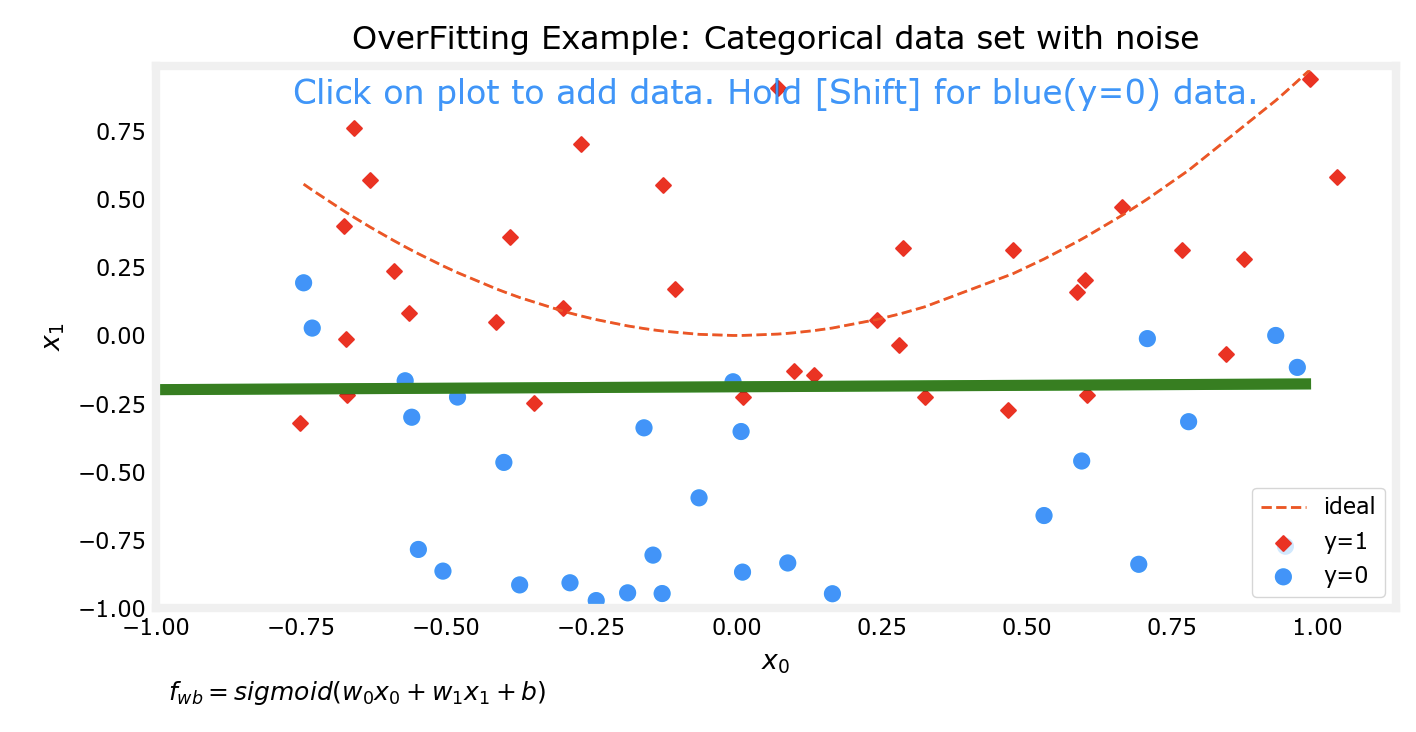
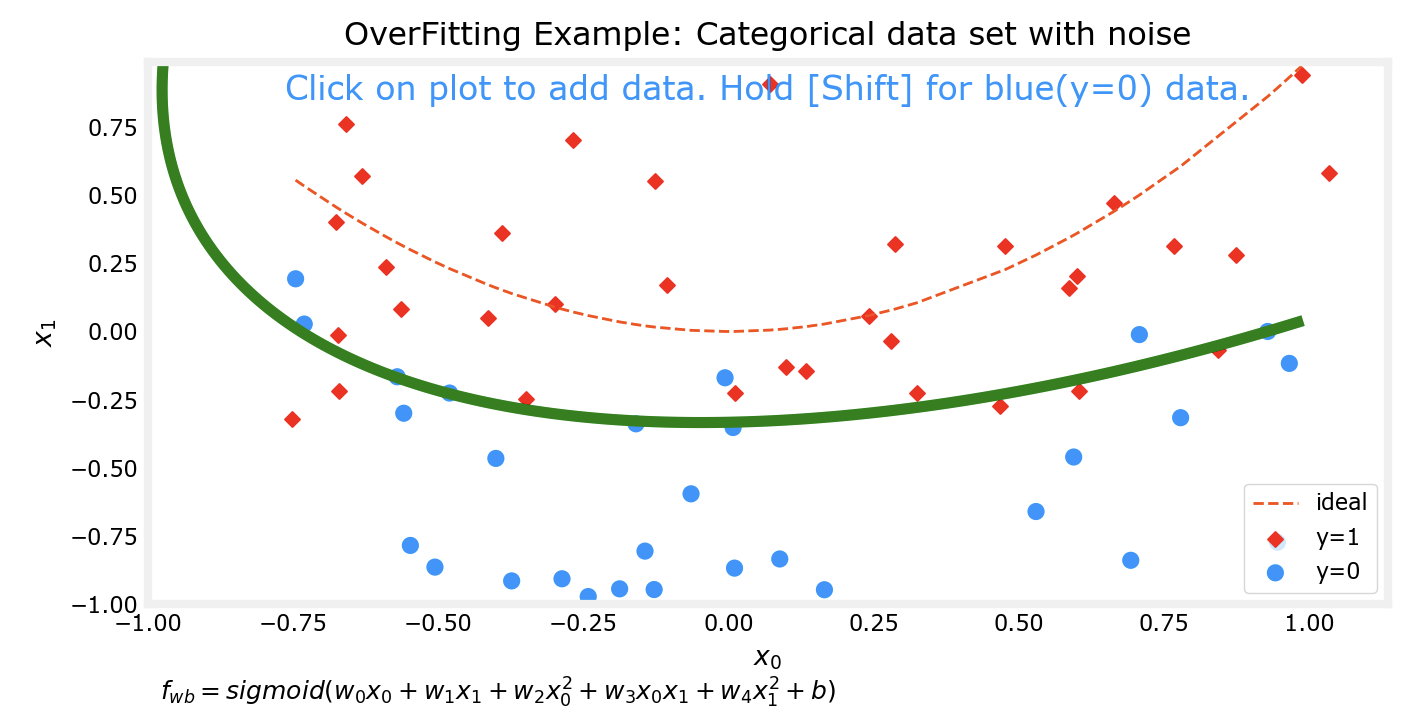
上边的四张图片分别代表了4个不同的模型对于同一数据集的拟合情况。可以看到,对于更为复杂的模型,对数据集的拟合程度越好。接下来我会对数据集进行一些改动,然后再次用相同次数的多项式分别对数据集进行拟合。
可以看出来,在对数据集行进了一些改动后,有两个现象:
上边两个较为低次的多项式模型对数据集的拟合程度仍然不如下面两个高次模型
对同一数据集进行微调前后,上边两个低次模型的拟合情况变化并不大;而下边两个高次模型在微调前后的拟合情况相差非常大
这个时候下面两个高次的模型实际上已经出现了过拟合 的现象。
模型应该随着数据集的变化而变化,但是不应该因为数据集中的某个或某几个样本而发生明显的巨大变化。比如样本有10000个,而仅仅在添加或更改了其中一个样本后,模型前后就发生了巨大的变化,尽管他能完美拟合数据集中的样本,但是该模型其实并不能有效预测一个合理的值。比如在10000个肿瘤的样本中,如果我们的模型是过拟合的,那么很有可能出现这样一种情况:变化之前的模型在拟合数据集后,预测大小0.1的肿瘤是良性的,这个时候又多了一个样本,由于过拟合现象的存在,该模型发生了很大变化,变化后它很有可能预测刚刚那个0.1的肿瘤是恶性的。而没有过拟合现象的模型仍然会认为0.1的肿瘤是良性的。而这对比一下,明显是没有过拟合模型更合理一些。
一些术语:欠拟合underfit<=>高偏差high bias、过拟合overfit<=>高方差high variance
解决过拟合
解决过拟合的方法有三种,分别是增加数据集的样本数量、选取和预测结果最相关的特征作为子集训练而不是训练整个数据集、正则化。
增加样本数量:局限性比较大,毕竟实际情况中样本的数量不可能想有多少就有多少
特征选择:这么做是为了选择与结果最为相关的特征进行训练,但是可能每一个特征都与预测结果直接相关,选择一个子集就会丢掉一些有用的特征
正则化:如果说特征选择是直接消灭掉不太相关的特征,那么正则化做的就不那么绝对,它会削弱这些不太相关特征的影响,算是一种弱化版的“特征选择”
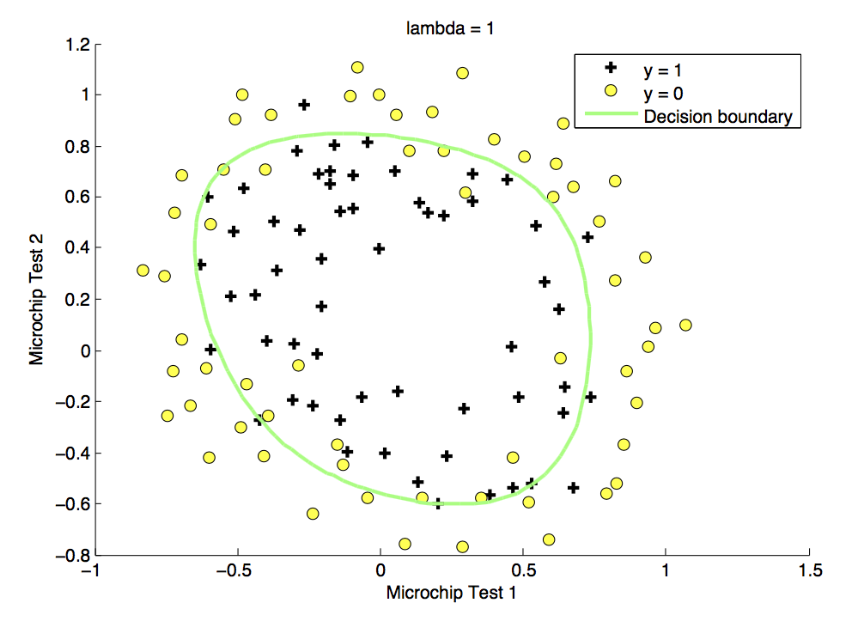
正则化实现的方法是对代价函数进行改进,在原有的代价函数基础上增加一个正则化项以减小不同特征对于模型的影响,一般来讲只需要将w ⃗ \vec{w} w b b b b b b λ 2 m ∑ j = 0 n − 1 w j 2 \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2 2 m λ ∑ j = 0 n − 1 w j 2 b b b λ 2 m b 2 \frac{\lambda}{2m}b^2 2 m λ b 2 λ \lambda λ
线性回归的正则化:
J ( w ⃗ , b ) = 1 2 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 + λ 2 m ∑ j = 0 n − 1 w j 2 J(\vec{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2
J ( w , b ) = 2 m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) 2 + 2 m λ j = 0 ∑ n − 1 w j 2
其中:
f w ⃗ , b ( x ⃗ ( i ) ) = w ⃗ ⋅ x ⃗ ( i ) + b f_{\vec{w},b}(\vec{x}^{(i)}) = \vec{w} \cdot \vec{x}^{(i)} + b
f w , b ( x ( i ) ) = w ⋅ x ( i ) + b
逻辑回归的正则化:
J ( w ⃗ , b ) = 1 m ∑ i = 0 m − 1 [ − y ( i ) log ( f w ⃗ , b ( x ⃗ ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] + λ 2 m ∑ j = 0 n − 1 w j 2 J(\vec{w},b) = \frac{1}{m} \sum_{i=0}^{m-1} \left[ -y^{(i)} \log\left(f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right) \right] + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2
J ( w , b ) = m 1 i = 0 ∑ m − 1 [ − y ( i ) log ( f w , b ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − f w , b ( x ( i ) ) ) ] + 2 m λ j = 0 ∑ n − 1 w j 2
其中:
f w ⃗ , b ( x ⃗ ( i ) ) = s i g m o i d ( w ⃗ ⋅ x ⃗ ( i ) + b ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}^{(i)}) = sigmoid(\vec{w} \cdot \vec{x}^{(i)} + b)= \frac{1}{1+e^{-(\vec{w} \cdot \vec{x} + b)}}
f w , b ( x ( i ) ) = s i g m o i d ( w ⋅ x ( i ) + b ) = 1 + e − ( w ⋅ x + b ) 1
对于改进后的代价函数,可以直观的看出λ \lambda λ λ \lambda λ w ⃗ \vec{w} w λ = 0 , \lambda=0, λ = 0 , w ⃗ \vec{w} w λ \lambda λ w ⃗ \vec{w} w b b b λ \lambda λ
正则化后再进行梯度下降
线性回归梯度下降:
repeat until convergence: { w j = w j − α ∂ J ( w ⃗ , b ) ∂ w j for j = 0,...,n-1 b = b − α ∂ J ( w ⃗ , b ) ∂ b } \begin{align*}
&\text{repeat until convergence:} \; \lbrace \\
& \; \; \;w_j = w_j - \alpha \frac{\partial J(\vec{w},b)}{\partial w_j} \; & \text{for j = 0,...,n-1} \\
& \; \; \; \; \;b = b - \alpha \frac{\partial J(\vec{w},b)}{\partial b} \\
&\rbrace
\end{align*} repeat until convergence: { w j = w j − α ∂ w j ∂ J ( w , b ) b = b − α ∂ b ∂ J ( w , b ) } for j = 0,...,n-1
其中:
J ( w ⃗ , b ) = 1 2 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 + λ 2 m ∑ j = 0 n − 1 w j 2 J(\vec{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2
J ( w , b ) = 2 m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) 2 + 2 m λ j = 0 ∑ n − 1 w j 2
于是:
∂ J ( w ⃗ , b ) ∂ w j = 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) + λ m w j ∂ J ( w ⃗ , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) \begin{align*}
\frac{\partial J(\vec{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})x_{j}^{(i)} + \frac{\lambda}{m} w_j \\
\frac{\partial J(\vec{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})
\end{align*} ∂ w j ∂ J ( w , b ) ∂ b ∂ J ( w , b ) = m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) + m λ w j = m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) )
逻辑回归梯度下降:
repeat until convergence: { w j = w j − α ∂ J ( w ⃗ , b ) ∂ w j for j = 0,...,n-1 b = b − α ∂ J ( w ⃗ , b ) ∂ b } \begin{align*}
&\text{repeat until convergence:} \; \lbrace \\
& \; \; \;w_j = w_j - \alpha \frac{\partial J(\vec{w},b)}{\partial w_j} \; & \text{for j = 0,...,n-1} \\
& \; \; \; \; \;b = b - \alpha \frac{\partial J(\vec{w},b)}{\partial b} \\
&\rbrace
\end{align*} repeat until convergence: { w j = w j − α ∂ w j ∂ J ( w , b ) b = b − α ∂ b ∂ J ( w , b ) } for j = 0,...,n-1
其中:
J ( w ⃗ , b ) = 1 m ∑ i = 0 m − 1 [ − y ( i ) log ( f w ⃗ , b ( x ⃗ ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] + λ 2 m ∑ j = 0 n − 1 w j 2 J(\vec{w},b) = \frac{1}{m} \sum_{i=0}^{m-1} \left[ -y^{(i)} \log\left(f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right) \right] + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2
J ( w , b ) = m 1 i = 0 ∑ m − 1 [ − y ( i ) log ( f w , b ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − f w , b ( x ( i ) ) ) ] + 2 m λ j = 0 ∑ n − 1 w j 2
于是:
∂ J ( w ⃗ , b ) ∂ w j = 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) + λ m w j ∂ J ( w ⃗ , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) \begin{align*}
\frac{\partial J(\vec{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})x_{j}^{(i)} + \frac{\lambda}{m} w_j \\
\frac{\partial J(\vec{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})
\end{align*} ∂ w j ∂ J ( w , b ) ∂ b ∂ J ( w , b ) = m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) + m λ w j = m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) )
同样,而这除了模型不一样,其余地方都是一样的。
一个问题
对正则化后的代价函数运行梯度下降时,对w ⃗ \vec{w} w
w j = w j − α ∂ J ( w ⃗ , b ) ∂ w j = ( 1 − α λ m ) w j − α 1 m ∑ i = 0 m − 1 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x j ( i ) w_j = w_j - \alpha \frac{\partial J(\vec{w},b)}{\partial w_j} =(1-\alpha \frac{\lambda}{m})w_j- \alpha \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)})x_{j}^{(i)} w j = w j − α ∂ w j ∂ J ( w , b ) = ( 1 − α m λ ) w j − α m 1 i = 0 ∑ m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i )
吴恩达依据α 、 λ \alpha 、\lambda α 、 λ w j w_j w j
第一:学习率α \alpha α λ \lambda λ α \alpha α
第二:第一项仅仅是一次迭代中的一部分,并没有计算完,还有第二项呢,第二项的正负也没办法确定吧,那每次迭代w j w_j w j
第三:正则化过程中参数w ⃗ \vec{w} w
有这个问题是因为在没有正则化的梯度下降中,我们的目的是寻找一组合适的而不是最小的w ⃗ 、 b \vec{w} 、b w 、 b w ⃗ 、 b \vec{w}、b w 、 b